Immaginiamo d'avere una popolazione di 100 pesci in uno stagno e controlliamo cosa succede se questi pesci hanno un incremento generazionale del 10%. La generazione successiva arriverà a 110 individui, poi salirà a 121, quindi a 133,1, etc, ma questo modo di prevedere l'andamento di una popolazione è troppo semplicistico, perchè non tiene conto dei soggetti che muoiono di morte naturale e del fatto che la popolazione non può crescere all'infinito, perchè anche il cibo dovrebbe aumentare all'infinito ;
a un certo punto non ci sarà più cibo sufficiente per tutti, conseguentemente la popolazione diminuirà. May però scoprì che usando questa formula matematica
(X.nuovo = r*X*(1-X)) con X <1
si otteneva un risultato più realistico, perchè questa equazione metteva in relazione l'abbondanza relativa (X) dei pesci con la disponibiltà relativa (1-X) del cibo
Amettiamo che i nostri 100 pesci abbiano a disposizione nel loro ecosistema 9900 larve, supponiamo poi che il peso totale dei pesci sia uguale al peso totale delle larve, perciò un ecosistema con una biomassa composta da 50% di predatori e da 50% di prede.
Se dividiamo il numero delle due popolazioni per il numero totale della biomassa (9900+100) abbiamo i numeri relativi all'abbondanza dei (pesci=100/10000)=0.01 e delle (larve = 9900/10000)= 0,99.
In questo modo dopo alcune generazioni, l'abbondanza X dei pesci sarà proporzionale all'abbondanza relativa delle larve, cioè x*(1-x).
A questo punto aggiungiamo una costante di proporzionalità (r) che rappresenta il tasso di crescita dei nostri pesci e la formula diventa X= r*X*(1-X)
Il valore massimo del tasso di crescita (r) è 4, questo perchè la somma dei numeri relativi di pesci e larve (0.01 + 0,99 = 1 ), perciò la (X) dovrà essere sempre inferiore < 1 e poichè, 1/2 biomassa è fatta di pesci e 1/2 di larve, abbiamo un prodotto di(0,5 * 0,5= 0.25 )ecco perchè il tasso di fecondità(r) deve avere un valore massimo di 4 dato che( 4 * 0.25 = 1).
Dato che (X) può assumere 1 come valore massimo, la formula richiede uno sviluppo frazionario.
Vediamo con un esempio di capire cosa succede ai nostri pesci usando questa formula.
Nota Con un tasso di fecondità (r = 1) la popolazione si estingue rapidamente, come logico se da una coppia di pesci si ha un solo pesciolino ogni generazione si dimezza e in poco tempo si estingue.
Ammettiamo ora che la popolazione iniziale sia di 0,02 pesci e che abbia un tasso di crescita (r = 2) Come vedi la popolazione dopo alcune generazioni si stabilizza su 0,5 ossia metà biomassa è fatta di pesci.
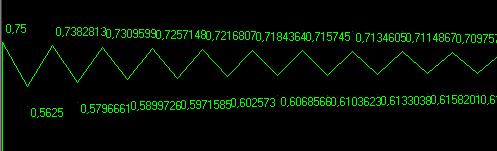
Con un tasso( r = 3)
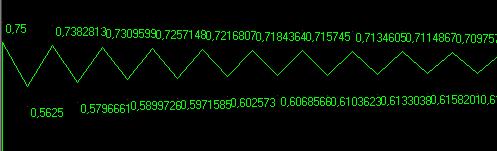
Il risultato dopo alcune generazioni si stabilizzerà attorno a due valori 0,631 e 0,699 vale a dire la biomassa dei pesci si alternerà su questi due valori.
Con un incremento di r vicino a( r = 3,5) si ha questo grafico.
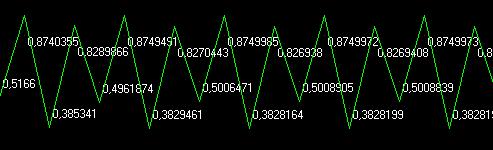
Come potete vedere la popolazione dei pesci si stabilizza su 4 livelli diversi,
Aumentando ancora un poco il valore a circa (r = 3,56 ) la popolazione si stabilizzerà su 8 valori, incrementando ulteriormente di pochissimo (r) ci saranno 16 valori stabili, poi 32, 64, 128 etc. ad ogni piccolo incremento di (r) si ha un raddoppio dei periodi stabili.
Improvvisamente quando (r) arriva a un valore di 3,56994571869 ha inizio il caos, la popolazione a ogni generazione cambia di numero in un modo completamente casuale, niente più periodi stabili.
Poi aumentando ulteriormente il valore di (r) ritornano dei brevi periodi di stabilità, prima con periodi pari 8; 10; 16; poi aumentando ancora (r) avremo periodi dispari, 3; 5; 7; 11;con relativi raddoppi del periodo. Alcuni di questi periodi stabili, sono molto brevi eppure hanno anche loro con il proprio raddopio,ecco perchè si chiama raddoppio del periodo. quello che colpisce è la loro improvvisa comparsa e scomparsa in mezzo al caos.
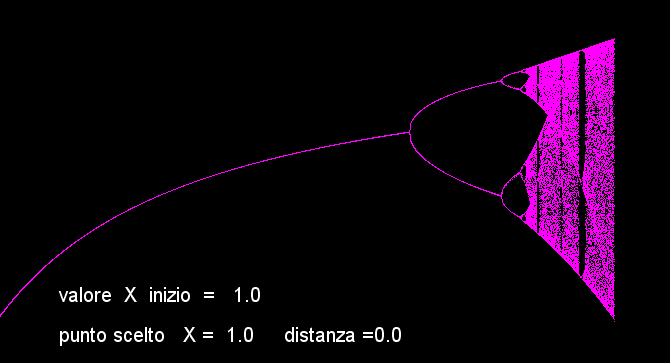
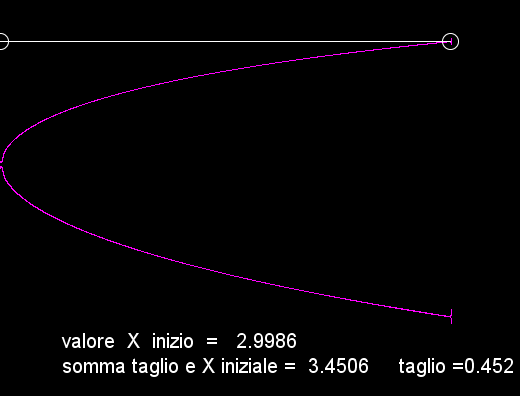
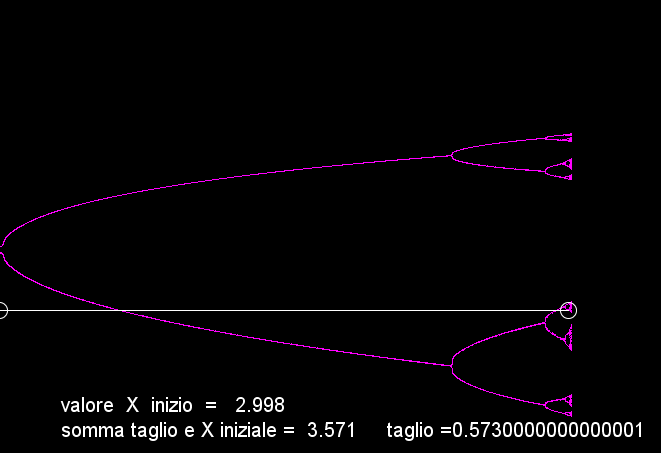
L'immagine qui sopra, rappresenta il nostro sistema attraverso lo spazio delle fasi
Si parte con un valore dell'incremento generazionale (r) pari a 1 -- e si arriva al valore massimo molto vicino a 4:
i valori di X che corrisponde al tasso di crescita iniziale (r), segue il nuovo valore di X scelto come tasso(r)di crescita situato al centro del cerchio bianco, mentre il terzo valore corrispondente alla linea bianca che li unisce ossia la distanza (r) tra i due punti. --
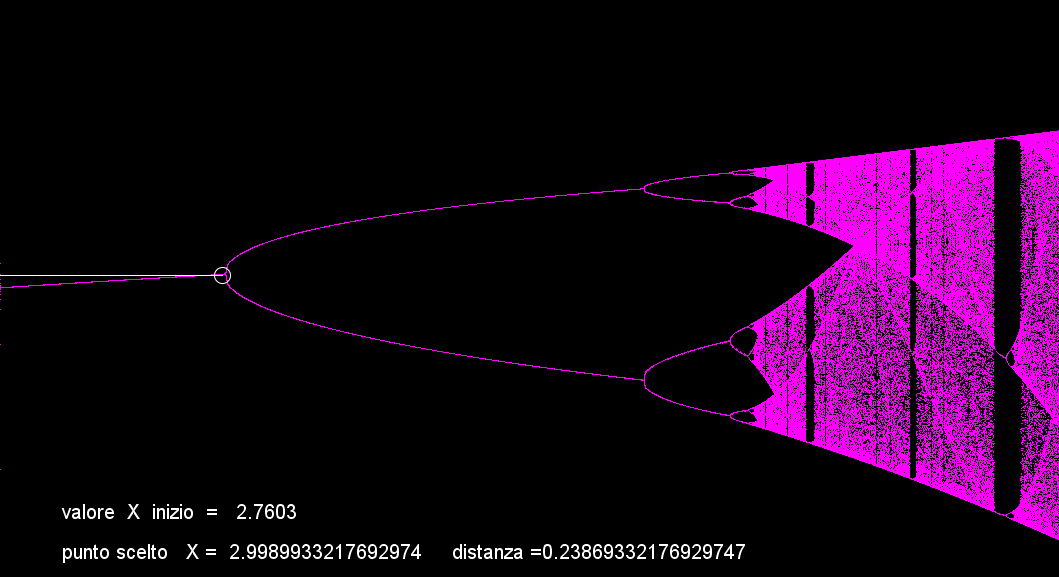
In questa immagine si parte da un valore di 2,7603 ed a ogni incremento di (r) la curva si sposta a destra, la popolazione aumenta senza grandi sobbalzi fino a quando giunge a un livello di (r) molto vicino a 3, nota i valori sotto il grafico; a questo punto la popolazione comincia a stabilizzarsi su due valori, una generazione aumenta, quella seguente diminuisce, il che corrisponde ai 2 valori stabili, visti nel grafico sopra, ecco perciò che la curva si divide e forma una specie di Y sdraiata, questo altalenarsi tra 2 valori prosegue fino a quando r raggiunge un valore vicino a 3.45....
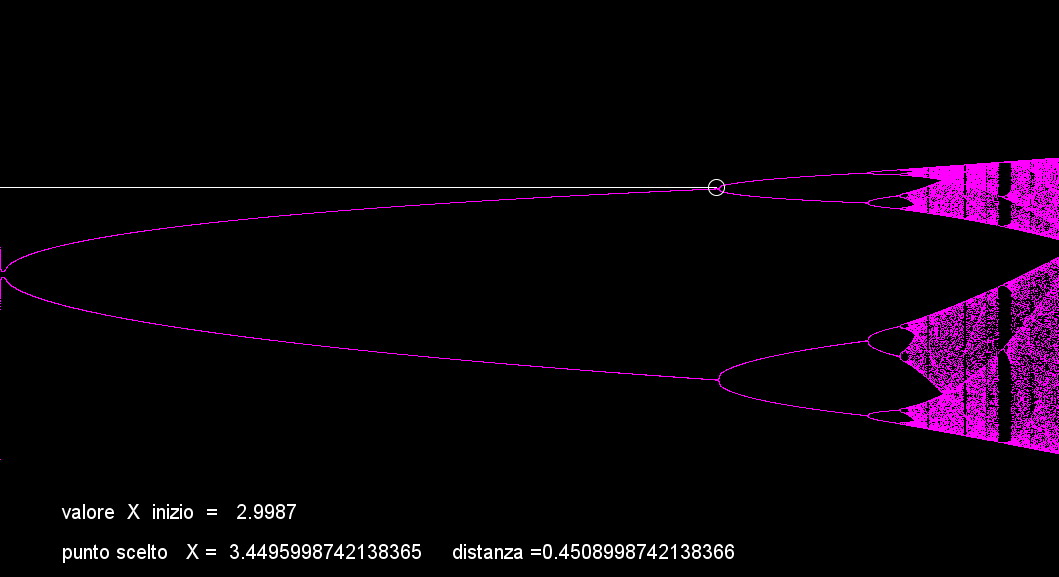
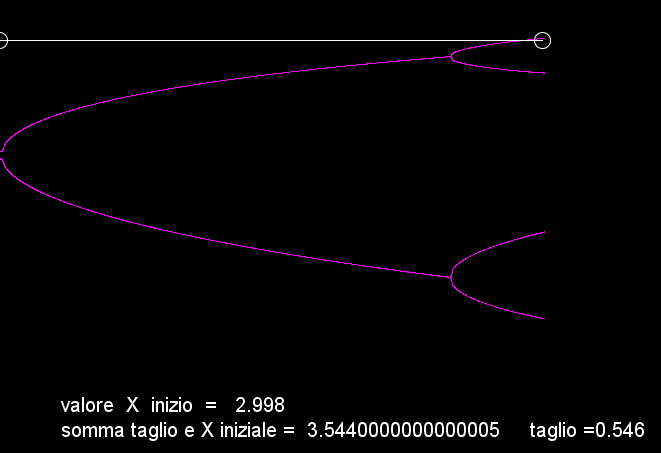
Infatti aumentando il tasso di crescita valore vicino a 3,45, notiamo che le due linee del si dividono a loro volta e diventano 4 (i 4 valori stabili visti sopra).
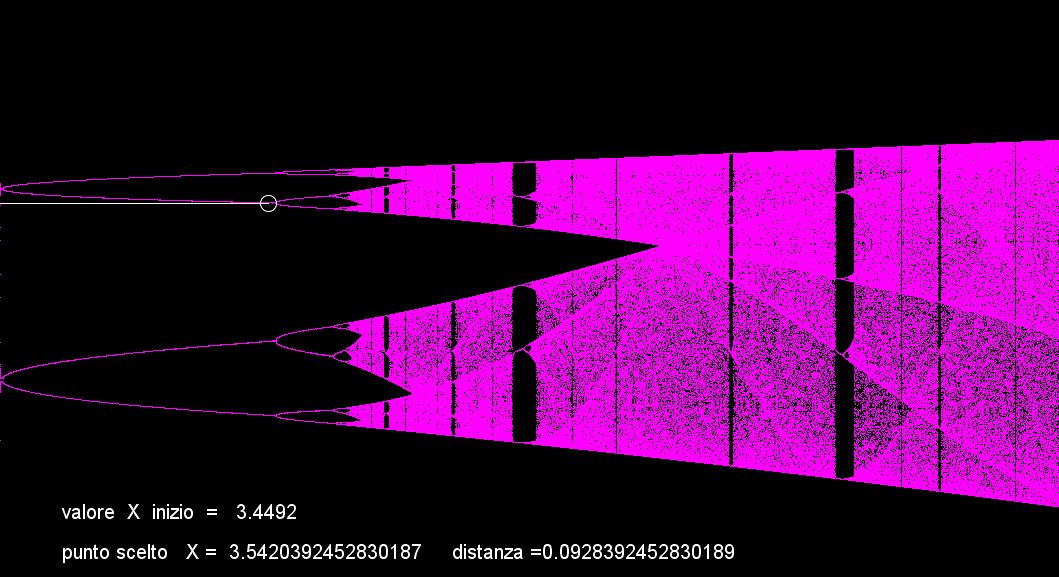
(r) a circa 3,54 le linee raddoppiano ancora e diventano 8 ma contemporaneamente diventano sempre più brevi, qui non si nota molto, perchè il grafico è stato stirato per evidenziare meglio gli 8 rami.
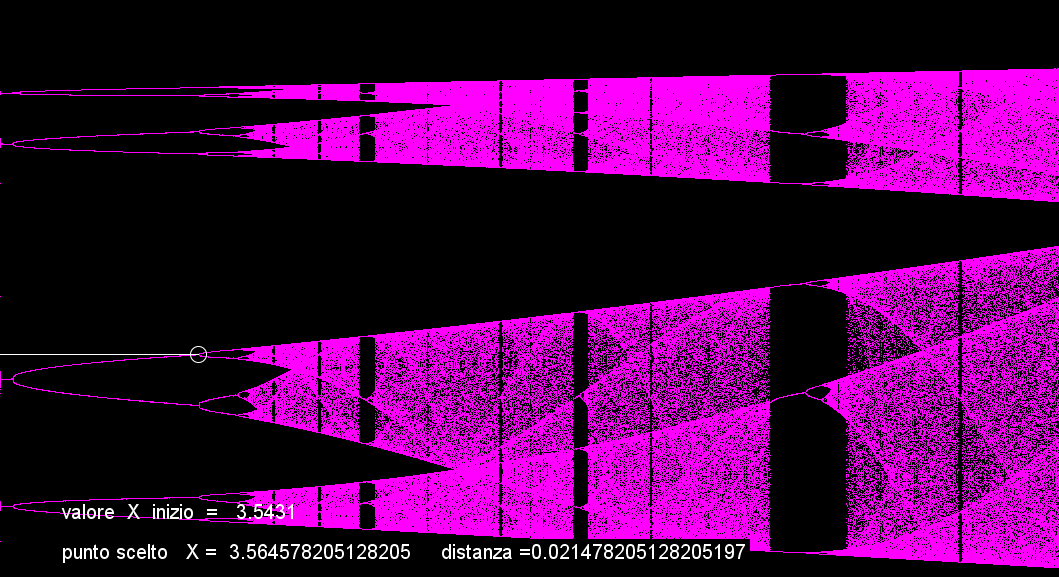
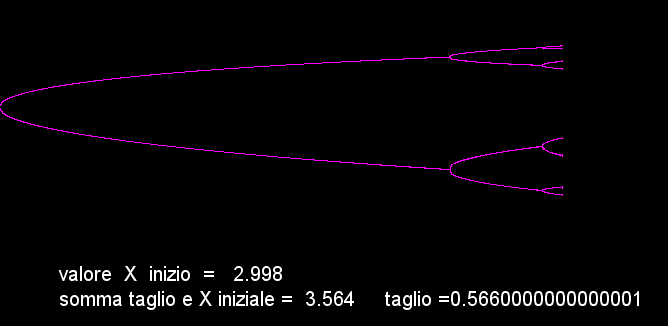
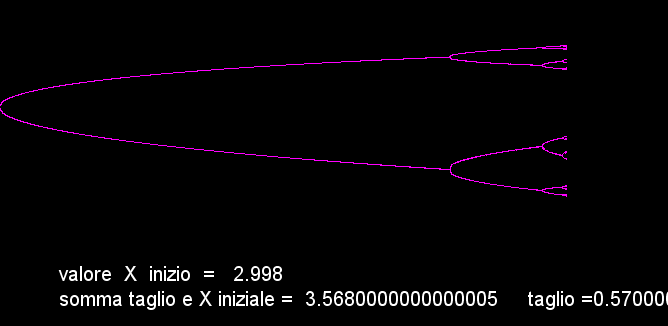
(D'ora in poi, dato che la distanza tra un raddoppio delle linee e l'altro diventa sempre più piccola, sarà difficile distinguere bene i particolari). Comunque continuando e portando (r) e circa 3,565 le linee diventano 16;
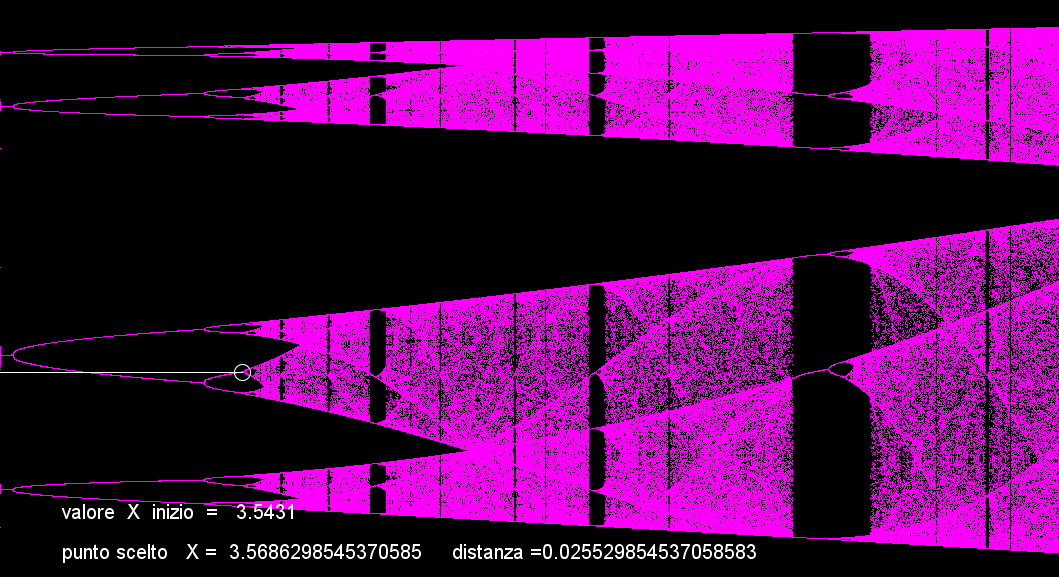
aumentando ulteriormente diventano 32;
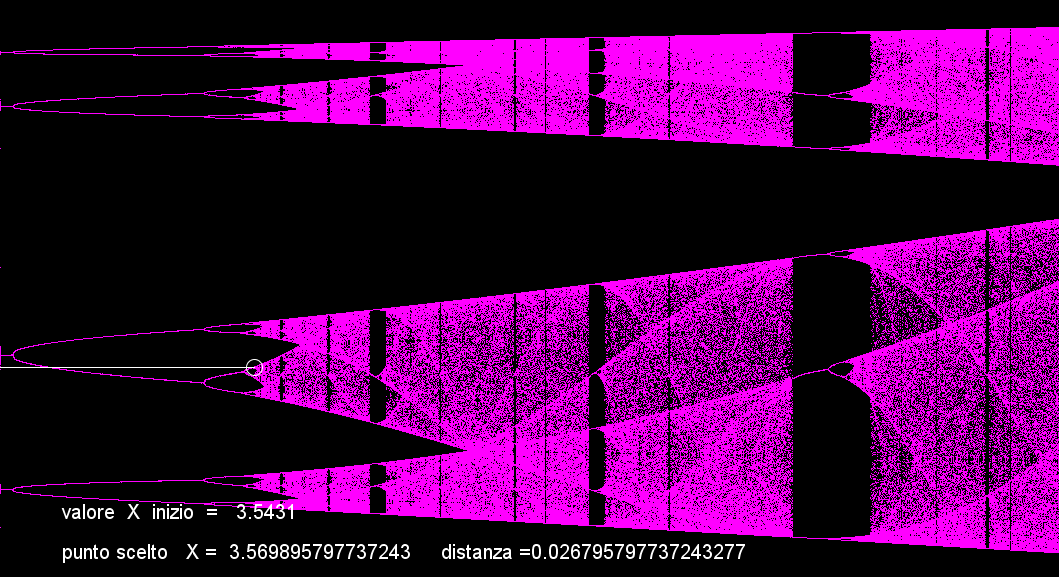
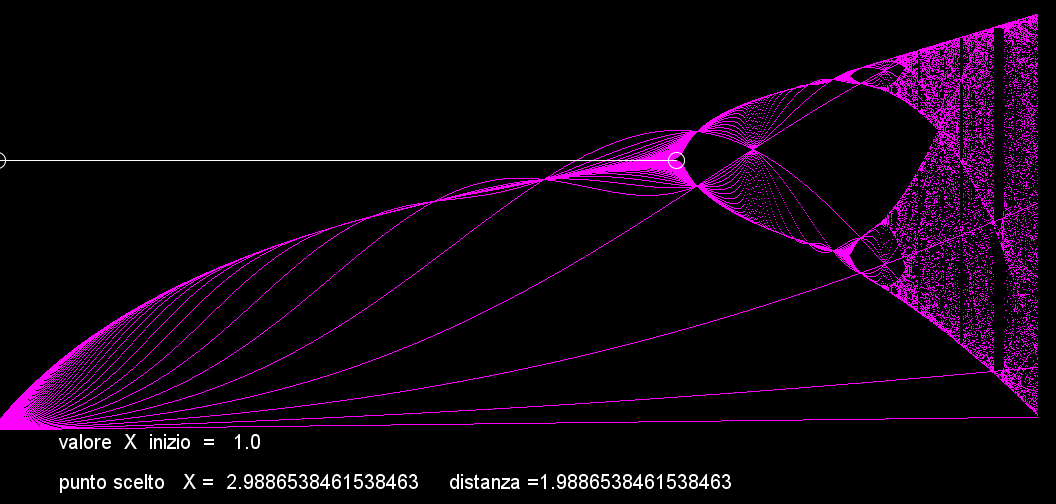
Infine, anche se è difficile vedere dove comincia esattamente il punto al centro del cerchietto bianco, arriva il caos, i punti si accumulano a caso senza alcuna stabilità.
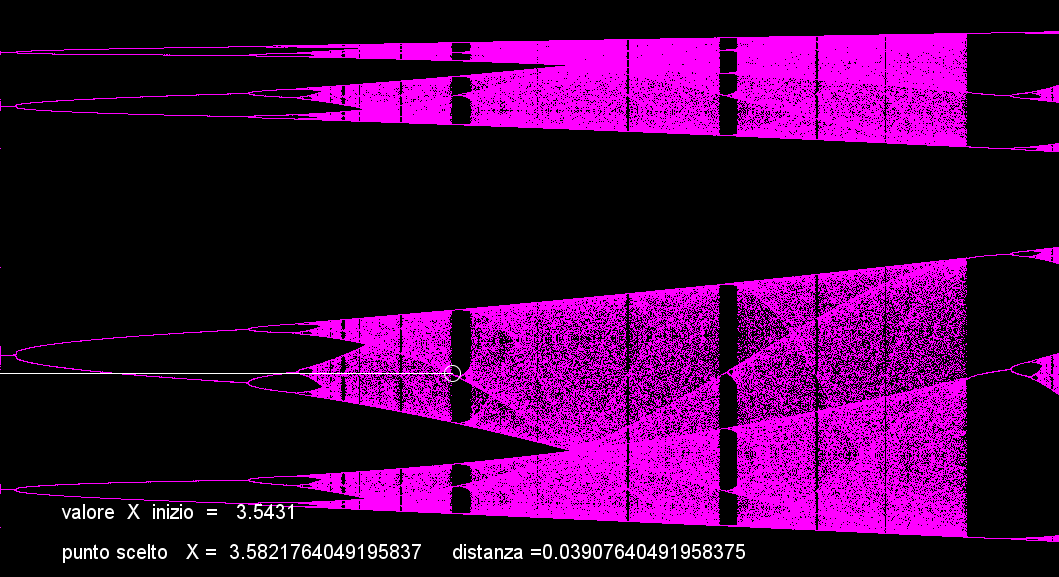
Ad ulteriori incrementi di (r) in mezzo al caos emergergono improvvisamente momenti di stabilità più o meno lunghi.
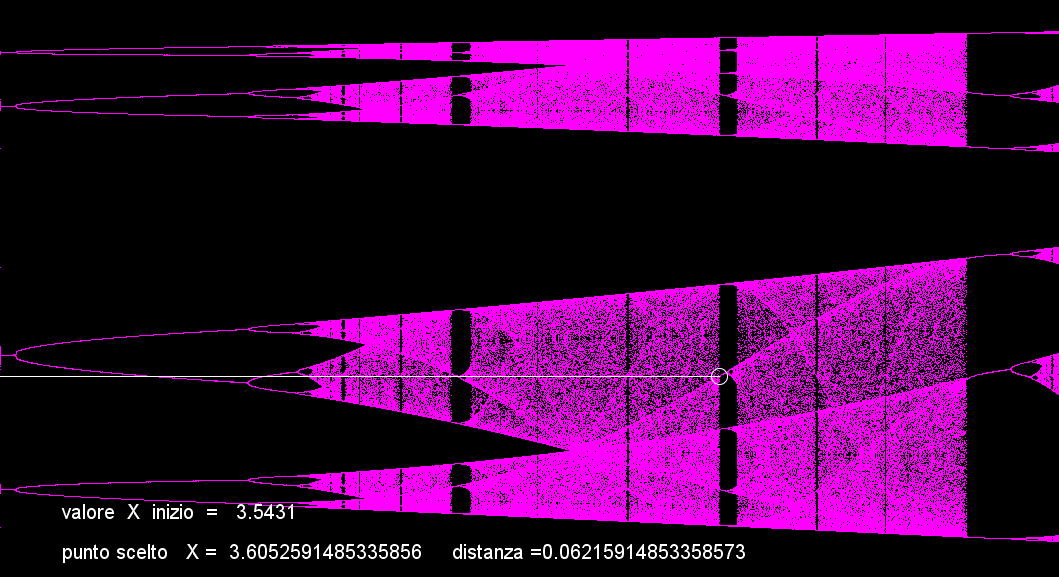
Questa immagine è simile alla precedente ma il centro del cerchio è puntato su (r) uguale a 3,605.. con un periodo 10= (5 ripetuto 2 vole). Nota anche il brevissimo periodo 14=(7*2) appena a sinistra del cerchio, oppure il periodo 12 = (6*2) abbastanza ampio ancora più a sinistra.
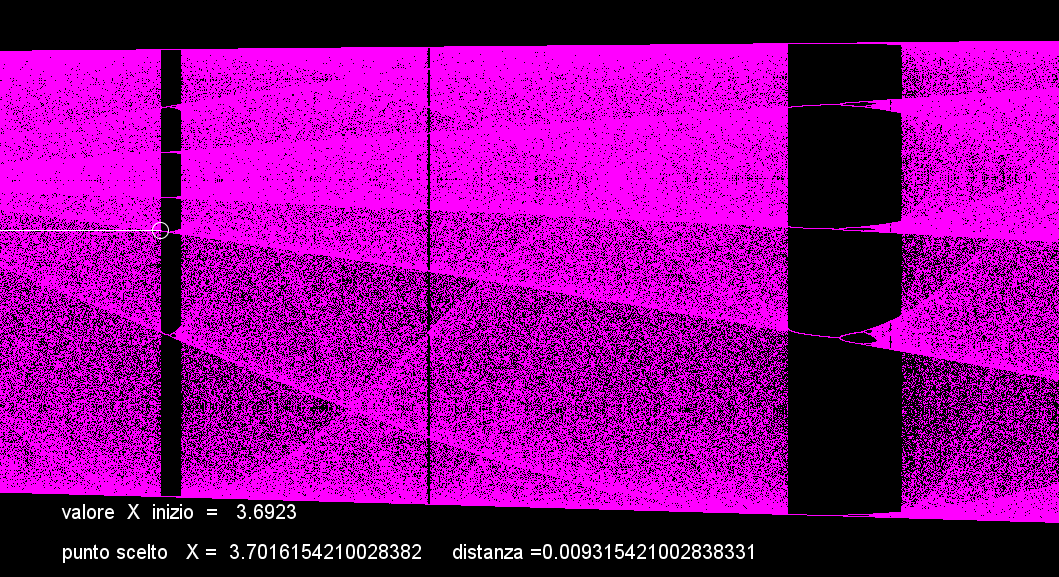
In questa immagine si parte dal punto (r) 3,6925 per arrivare al centro del cerchio nel punto 3,7016... come vedi la distanza tra questi 2 punti è solo 0,00093 questo indica che l'immagine è stata stirata moltissimo per evidenziare come il comportamento caotico nasconda al suo interno dei brevissimi periodi di distabilità, quello di questo esempio ha un periodo 7 con i relativi raddoppi, subito dopo, appena visibile c'è un periodo 9 che se ulteriormente stirato mostrerebbe i suoi raddoppi del periodo.
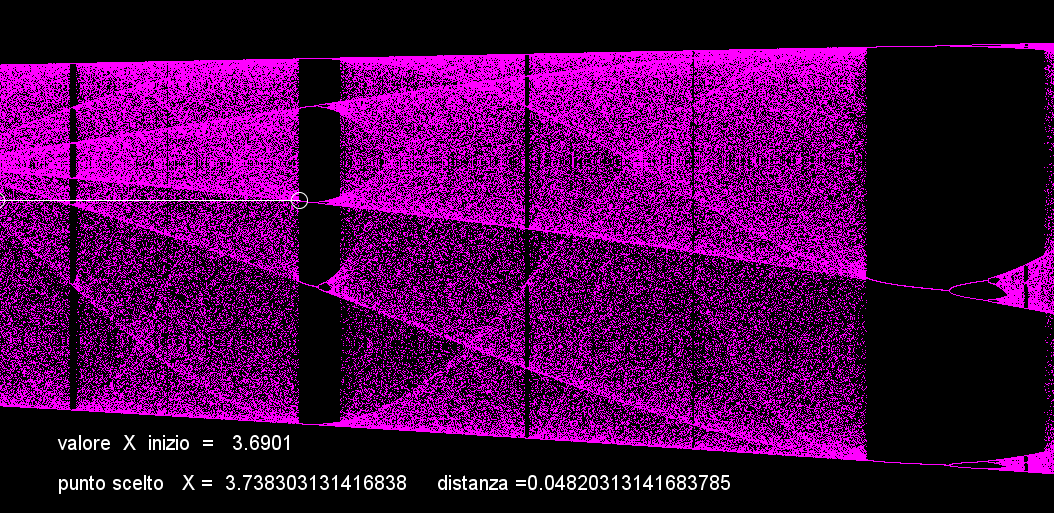
Questa immagine è leggermete meno stirata della precedente, i cerchio bianco è puntato sul periodo 5 lo stesso visto anche nell'immagine sopra, questo periodo è seguito da 2 ulteriori periodi 7 seguiti a loro volta da un periodo 3 abbastanza lungo.
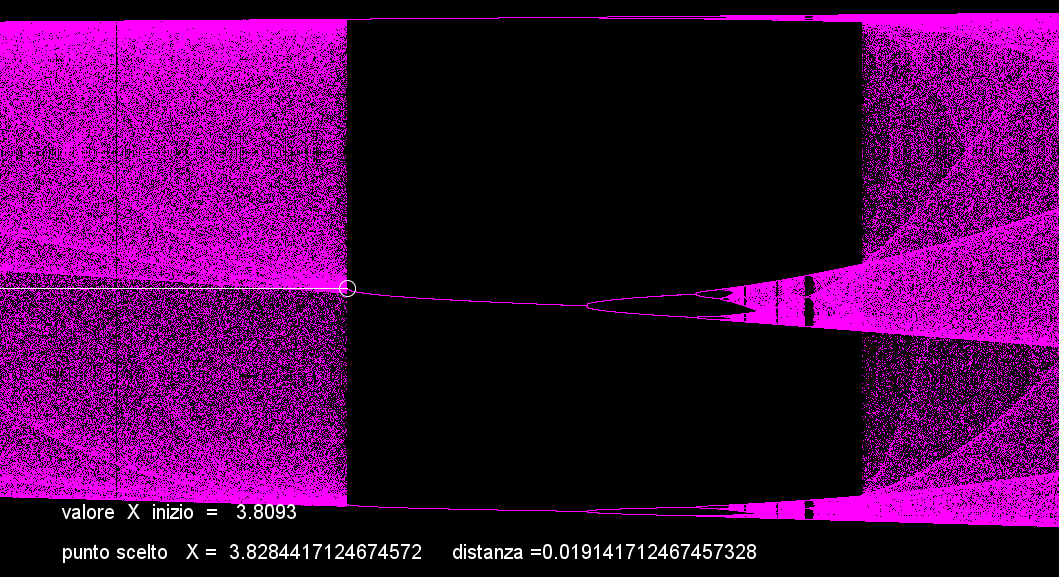
Questa immagine molto stirata, mostra in modo inequivocabile il comportamento frattale che nasce da questa formula, si vede in modo chiaro che ogni periodo è seguito da alcuni raddoppiamenti che sfociano nel caos.
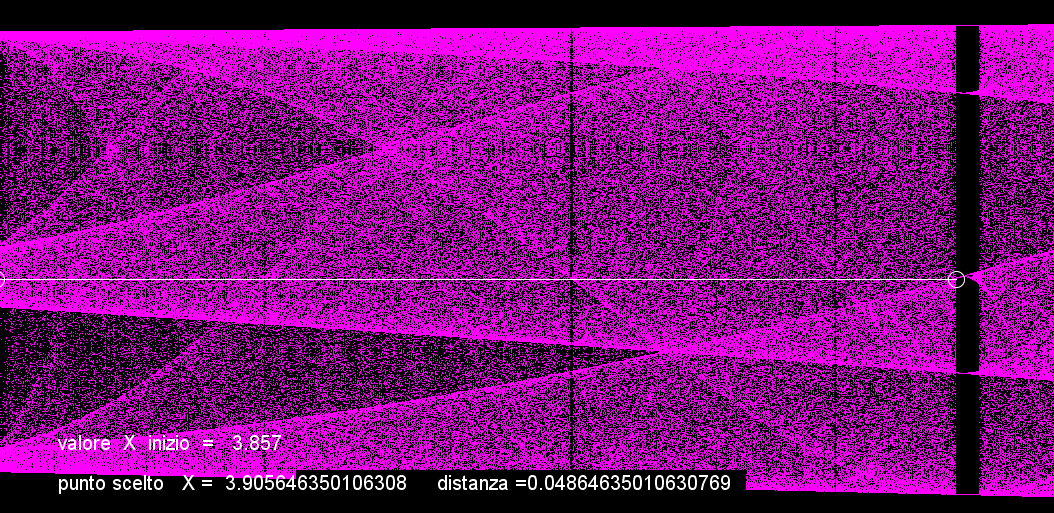
Questa immagine mostra che aumentando il valore di (r) fin a 3,9056.. abbiamo un periodo 5 abbastanza stabile, ma anche qui puoi notare che in precedenza ci sono dei brevissimi periodi di stabilità in mezzo al caos.